Lab3-CUDA 使用基础
实验简介
1
2
3
4
5
6
7
| 通用矩阵乘法(General matrix multiply, GEMM)是 BLAS 中经典的子程序之一。[2] 作为当今科学计算最常见的
计算任务之一,GEMM 需要实现一个非常高效的矩阵乘法。优化 GEMM 也是 HPC 界非常基础的任务。
本次实验需要你使用 CUDA 完成一个高性能 GEMM 实现。
你可以自由选择使用 CUDA Runtime API 或者 CUDA Driver API 进行编程,但不能调用高性能计算的 Library 代
替你自己实现 GEMM。本实验推荐采用 CUDA Runtime API,使用更加简单方便,相较 Driver 几乎不损失性能。
|
基准代码
1
2
3
4
5
6
7
8
9
10
11
12
13
| __global__ void MultipleCudaKernel(const double *__restrict__ a,
const double *__restrict__ b,
double *__restrict__ result)
{
const int i = blockIdx.x * block_size + threadIdx.x;
const int j = blockIdx.y * block_size + threadIdx.y;
if (i < size && j < size) {
result(i, j) = 0;
for (int k = 0; k < size; ++k) {
result(i, j) += a(i, k) * b(k, j);
}
}
}
|
一、利用 Shared Memory 优化
中间代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| __global__ void MultipleCudaKernel(const double *__restrict__ a,
const double *__restrict__ b,
double *__restrict__ result)
{
const int i = blockIdx.x * block_size + threadIdx.x;
const int j = blockIdx.y * block_size + threadIdx.y;
__shared__ double shared_a[block_size][block_size];
__shared__ double shared_b[block_size][block_size];
double sum = 0.0;
for (int m = 0; m < (size + block_size - 1) / block_size; m++) {
if (i < size && threadIdx.y + m * block_size < size) {
shared_a[threadIdx.x][threadIdx.y] = a[i * size + m * block_size + threadIdx.y];
} else {
shared_a[threadIdx.x][threadIdx.y] = 0.0;
}
if (j < size && threadIdx.x + m * block_size < size) {
shared_b[threadIdx.x][threadIdx.y] = b[j + size * (threadIdx.x + m * block_size)];
} else {
shared_b[threadIdx.x][threadIdx.y] = 0.0;
}
__syncthreads();
for (int n = 0; n < block_size; n++) {
sum += shared_a[threadIdx.x][n] * shared_b[n][threadIdx.y];
__syncthreads();
}
}
if (i < size && j < size) result(i, j) = sum;
}
|
思路分析
使用分块矩阵的思想,每一个 block
对应一个矩阵块,其中每一个线程来计算对应矩阵元素的值
\[
A =
\begin{pmatrix}
A_{0,0} & \cdots & A_{0,K-1} \\
\vdots & & \vdots \\
A_{K-1,0} & \cdots & A_{K-1,K-1} \\
\end{pmatrix}
\quad
B=
\begin{pmatrix}
B_{0,0} & \cdots & B_{0,K-1} \\
\vdots & & \vdots \\
B_{K-1,0} & \cdots & B_{K-1,K-1} \\
\end{pmatrix}
\] \[
C=
\begin{pmatrix}
C_{0,0} & \cdots & C_{0,K-1} \\
\vdots & & \vdots \\
C_{K-1,0} & \cdots & C_{K-1,K-1} \\
\end{pmatrix}
\ ,\ \ \text{其中}
C_{ij} = \sum_{k=0}^{N-1} A_{ik}B_{kj}
\]
代码中的 shared_a 和 shared_b
就是一个个小的矩阵块,将数据从 global memory 上迁移到 shared memory
上加速访存速度,来实现矩阵运算的优化。其中 shared_a 对应
a[j * size + m * block_size + threadIdx.x]
即一横行的矩阵块,shared_b
则相应为一纵列的矩阵块,这就是第一个循环;第二个循环就是用单个矩阵元素做简单矩阵运算。
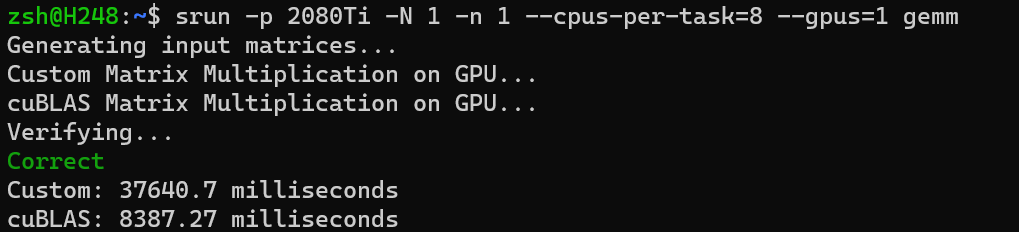
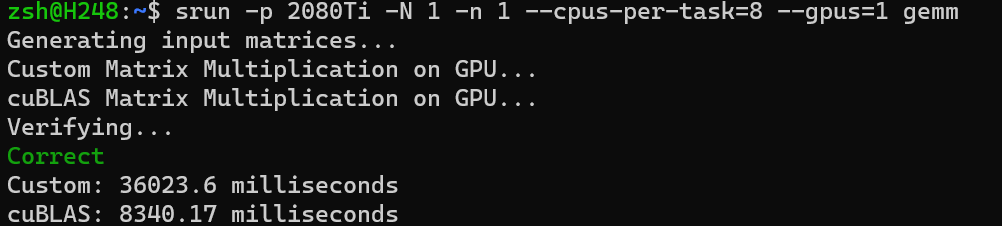
相对性能
完成 Shared Memory
部分后在集群上运行的效率似乎并没有显著提升,但在我自己的电脑上相较基准代码却有数倍的加速。(大雾
完成 CUDA 加速
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| __global__ void MultipleCudaKernel(const double *__restrict__ a,
const double *__restrict__ b,
double *__restrict__ result)
{
const int i = blockIdx.x * block_size + threadIdx.x;
const int j = blockIdx.y * block_size + threadIdx.y;
__shared__ double shared_a[block_size][block_size];
__shared__ double shared_b[block_size][block_size];
double sum = 0.0;
for (int m = 0; m < (size + block_size - 1) / block_size; m++) {
if (j < size && threadIdx.x + m * block_size < size) {
shared_a[threadIdx.y][threadIdx.x] = a[j * size + m * block_size + threadIdx.x];
} else {
shared_a[threadIdx.y][threadIdx.x] = 0.0;
}
if (i < size && threadIdx.y + m * block_size < size) {
shared_b[threadIdx.y][threadIdx.x] = b[i + size * (threadIdx.y + m * block_size)];
} else {
shared_b[threadIdx.y][threadIdx.x] = 0.0;
}
__syncthreads();
for (int n = 0; n < block_size; n++) {
sum += shared_a[threadIdx.y][n] * shared_b[n][threadIdx.x];
__syncthreads();
}
}
if (i < size && j < size) result(j, i) = sum;
}
|
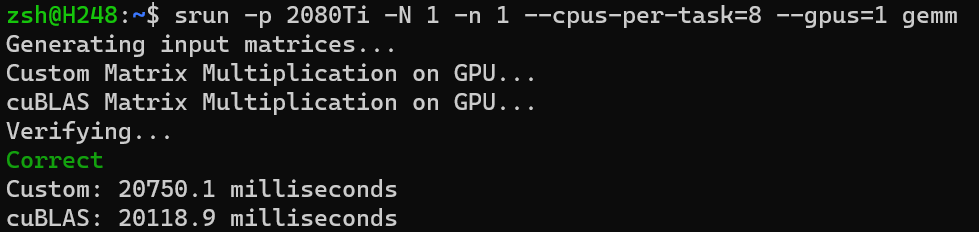
\[
Relative\ Performance = \frac{Your\ Time\ Cost}{cuBLAS\ Time\ Cost} =
\frac{20750.1}{20118.9} \approx 1.03
\]
二、通过 Tensor Core 计算
引用头文件和命名空间
1
2
| #include <mma.h>
using namespace nvcuda;
|
MutiplyCudaKernel 函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #define M_frag 8
#define N_frag 8
#define K_frag 4
__global__ void MultipleCudaKernel(const double *__restrict__ a,
const double *__restrict__ b,
double *__restrict__ result)
{
int warpM = (blockIdx.x * blockDim.x + threadIdx.x) / warpSize;
int warpN = (blockIdx.y * blockDim.y + threadIdx.y);
wmma::fragment<wmma::matrix_a, M_frag, N_frag, K_frag, double, wmma::row_major> a_frag;
wmma::fragment<wmma::matrix_b, M_frag, N_frag, K_frag, double, wmma::row_major> b_frag;
wmma::fragment<wmma::accumulator, M_frag, N_frag, K_frag, double> result_frag;
wmma::fill_fragment(result_frag, 0.0);
for (int i = 0; i < better_size; i += K_frag) {
int aRow = warpM * M_frag;
int aCol = i;
int bRow = i;
int bCol = warpN * N_frag;
if (aRow < better_size && aCol < better_size && bRow < better_size && bCol < better_size) {
wmma::load_matrix_sync(a_frag, a + aCol + aRow * better_size, better_size);
wmma::load_matrix_sync(b_frag, b + bCol + bRow * better_size, better_size);
wmma::mma_sync(result_frag, a_frag, b_frag, result_frag);
}
}
int Row = warpM * M_frag;
int Col = warpN * N_frag;
if (Row < better_size && Col < better_size) {
wmma::store_matrix_sync(result + Col + Row * better_size, result_frag, better_size, wmma::mem_row_major);
}
}
|
边界处理与线程分配
边界处理
因为 Tensor Core 对与矩阵形状有特殊的要求(本次实验中
double 类型的 Tensor Core 要求 tile 的形状 \(M \times N \times K\) 必须为 \(8 \times 8 \times 4\)),
所以矩阵的边长必须为 8
的整数倍。这意味着非整数倍的矩阵必须进行边界处理,为了便于处理,这里可以延伸矩阵。原有位置数据不变,外围多增加一圈
0 。
1
2
| #define division(a, b) (((a) % (b)) ? ((a) / (b) + 1) : ((a) / (b)))
#define better_size (division(size, 8) * 8)
|
线程分配
Tensor Core 计算是以 warp 为单位进行的,因此一个 warp 需要对应一个
\(M \times N \times K\) 矩阵块。32 个
thread 一组为一个 warp ,因此 block.x 必须为 32
的倍数,其余并无特殊要求。
1
2
3
| dim3 block(64, 2);
dim3 grid((division(better_size, WMMA_M * block2.x / 32)),
division(better_size, WMMA_N * block2.y));
|
完成 CUDA 加速
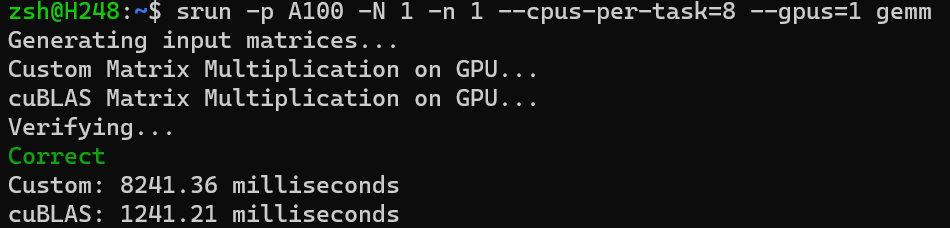
\[
Relative\ Performance = \frac{Your\ Time\ Cost}{cuBLAS\ Time\ Cost} =
\frac{8241.36}{1241.21} \approx 6.64
\]