Lab4-PCG Solver

实验简介

1
2
3
4
5
PCG 是一种利用多次迭代对方程组进行求解的方法。相比于使用直接法求解方程组，其对于存储空间的要求不高且扩展
性良好，在涉及方程组求解的科学计算应用中具有一定的优势

本次实验中，你需要使用OpenMP和MPI在多节点CPU集群上对串行PCG程序进行加速，并使用Profile工具进行性能分析。
使用Fortran完成本次实验将可以获得Bonus。

基准代码

访存优化

程序中对于内存的访问几乎全为线性，因此没有进行数组封装。矩阵分块和循环展开的操作也是配合 OpenMP 和 MPI 一起使用进行优化的。

SIMD

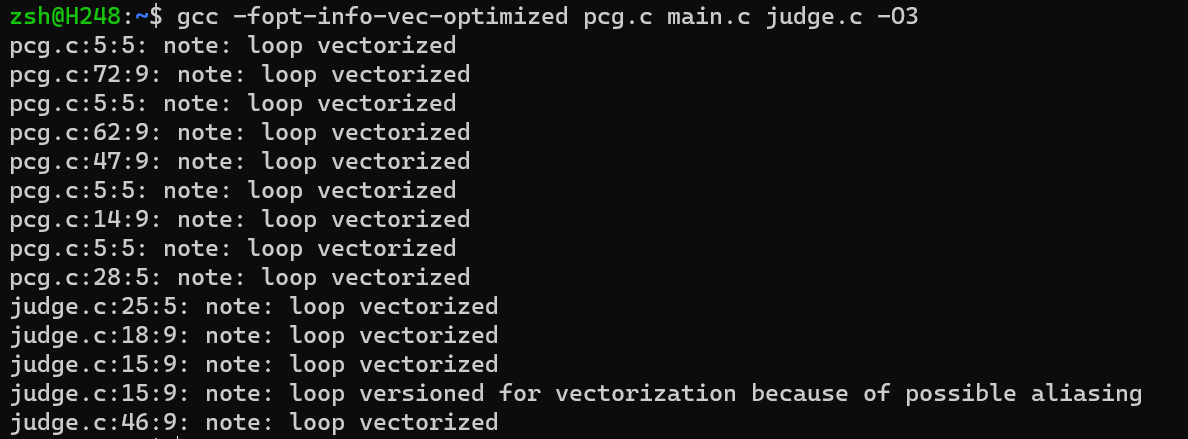
通过 gcc -fopt-info-vec-optimized pcg.c main.c judge.c -O3 命令来观察 -O3 编译选项下的自动向量化情况，可以知道的是大部分循环已经被自动向量化。

OpenMP

PCG 算法中包括点积、矩阵乘法和加法这些并行性质良好的运算，因此对于简单的一层 for 循环，我们可以直接使用 OpenMP 进行循环展开。

1
2
3
4
5
6
7
8
double dot(double a[], double b[], int size){
    double dot_sum = 0;
    #pragma omp parallel for reduction(+:dot_sum)
    for (int i = 0; i < size; ++i) {
        dot_sum += a[i] * b[i];
    }
    return dot_sum;
}
1
2
3
4
#pragma omp parallel for
for (int i = 0; i < size; ++i) {
    z[i] = r[i] / A[i][i];
}

仅仅这样循环展开并没有提升效率，用 #pragma omp parallel for simd 的话效率有略微提升。

MPI

并行化 PCG 算法，主要并行的部分是矩阵乘法部分，也就是基准代码中的 dot 和 MatrixMulVec 函数，因此可以让主进程去跑迭代循环，其中的计算分发到从进程上执行。

迭代中复杂度最高的运算就是 MatrixMulVec 函数，这是一个 \(\rm{size} \times \rm{size}\) 的矩阵和 \(\rm{size} \times 1\) 的向量作乘法运算，因此我们可以把 \(\rm{size} \times \rm{size}\) 的矩阵进行分块，每块交给一个进程去做计算，最后用 MPI 通信结果。(用 OpenMPI 竟然比 IntelMPI 快不少 ×)

1
2
3
4
5
6
7
8
9
void MPI_MatrixMulVec(int begin_row, int end_row, int size, double A[][size], double x[]) {
    for (int i = begin_row; i <= end_row; ++i) {
        double ans = 0.0;
        for (int j = 0; j < size; ++j) {
            ans += A[i][j] * x[j];
        }
        MPI_Send(&ans, 1, MPI_DOUBLE, master, i, MPI_COMM_WORLD);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#define master 0
#define block_rows (size / (numprocs - 1) + 1)
#define min(a,b) (a) > (b) ? (b) : (a)

void PCG(int size, double A[][size], double b[]) {

    int rank, numprocs;
    MPI_Status status;
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &numprocs);

    if (rank == master) {
        start_timer();

        double r[size], x[size], z[size], p[size];
        double alpha, beta, gamma, r_dot_z, A_dot_p[size];

        /* initialization */
        for (int i = 0; i < size; ++i) {
            x[i] = 0;
            r[i] = b[i];
            z[i] = r[i] / A[i][i];
            p[i] = z[i];
        }

        for (int i = 0; i < size; i++) {
            MPI_Bcast(A[i], size, MPI_DOUBLE, master, MPI_COMM_WORLD);
        } // 广播矩阵 A

        /* solve */
        int iter = 0;
        double loss = 0;
        r_dot_z = dot(r, z, size);
        do {            
            /* A * p_k */
            MPI_Bcast(p, size, MPI_DOUBLE, master, MPI_COMM_WORLD);
            // 每次迭代广播向量 p

            for (int i = 0; i < size; i++) {
                double ans;
                MPI_Recv(&ans, 1, MPI_DOUBLE, MPI_ANY_SOURCE, MPI_ANY_TAG, MPI_COMM_WORLD, &status);
                A_dot_p[status.MPI_TAG] = ans;
            } // 接收 ans 并以 tag 为索引存储到 A_dot_p 中

            /*
            省略 PCG 算法过程
            */

            for (int i = 1; i < numprocs; i++) {
                MPI_Send(&loss, 1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD);
            }
        } while (++iter < MAXITER && loss > EPI);

        check(size, A, x, b, iter);
    } else {
        int iter = 0;
        int begin_row = (rank - 1) * block_rows, end_row = min(rank * block_rows - 1, size - 1);
        double loss = 0;
        double p[size];
        for (int i = 0; i < size; i++) {
            MPI_Bcast(A[i], size, MPI_DOUBLE, master, MPI_COMM_WORLD);
        } // 接收矩阵 A

        do {
            /* A * p_k */
            MPI_Bcast(p, size, MPI_DOUBLE, master, MPI_COMM_WORLD);
            // 每次迭代更新向量 p
            MatrixMulVec(begin_row, end_row, size, A, p);
            // 矩阵运算并发送结果
            MPI_Recv(&loss, 1, MPI_DOUBLE, master, 0, MPI_COMM_WORLD, &status);
            // 接收 loss 用于判断循环结束条件
        } while (++iter < MAXITER && loss > EPI);
    }
}

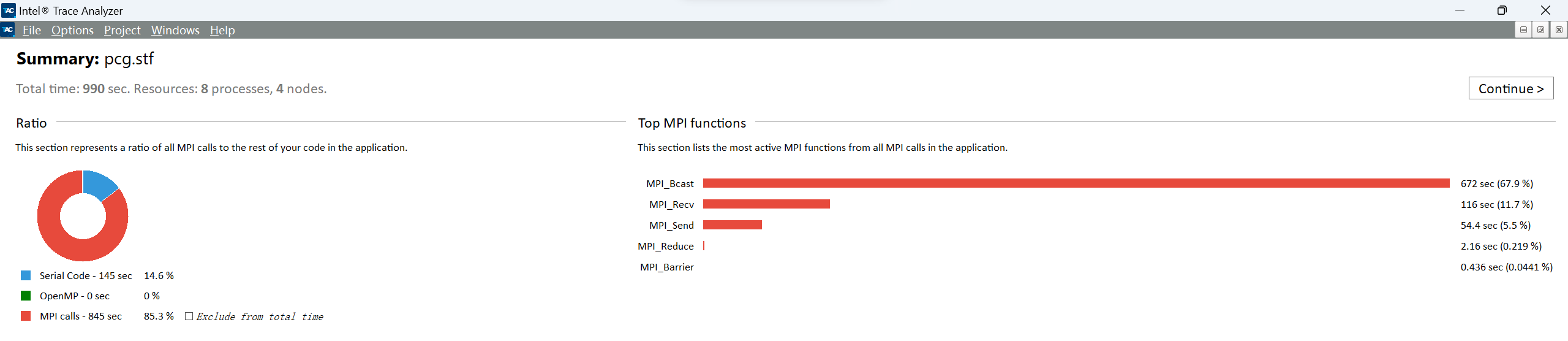
耗时最多的三个MPI函数分别是 MPI_Bcast 、 MPI_Recv 、 MPI_Send，程序在MPI上消耗的总时间为 845 sec。

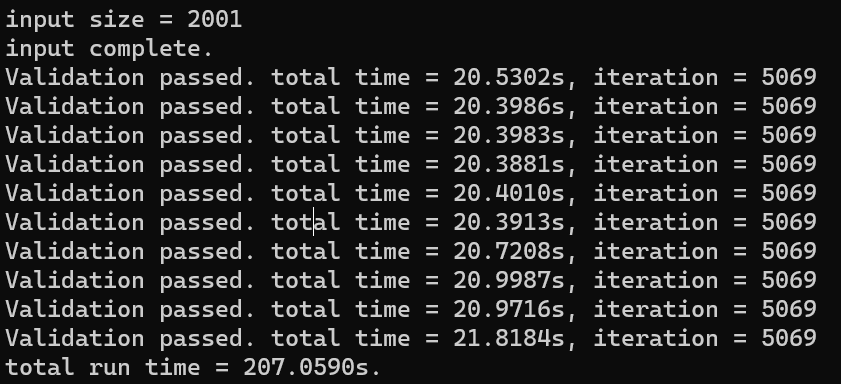
完成 PCG 加速

  • 修改代码

    显然算完矩阵乘法后从进程闲着没事干，所以可以并行化 do-while 循环里的其他运算。在尝试一个个单独并行化后发现，对于向量加减 mpi 的作用为负优化，只有在 dot 运算上有略微加速。

    dot 函数的并行化很简单，只需要分段计算再用 MPI_Reduce 归约起来就可以了。这里只优化了上面的点积，是因为下面的点积如果要进行优化需要 MPI_Bcast 两组数据。

    1
    2
    3
    4
    // 主进程
    MPI_Bcast(A_dot_p, size, MPI_DOUBLE, master, MPI_COMM_WORLD);
    MPI_Reduce(&other_dot, &master_dot, 1, MPI_DOUBLE, MPI_SUM, master, MPI_COMM_WORLD);
    alpha = r_dot_z / master_dot;

    1
    2
    3
    4
    // 从进程
    MPI_Bcast(A_dot_p, size, MPI_DOUBLE, master, MPI_COMM_WORLD);
    other_dot = MPI_dot(begin_row, end_row, p, A_dot_p);
    MPI_Reduce(&other_dot, &master_dot, 1, MPI_DOUBLE, MPI_SUM, master, MPI_COMM_WORLD);

  • 编译参数 Makefile

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
CC = mpicc
CFLAGS = -fopenmp -O3 -march=native

.PHONY = pcg

pcg: main.o judge.o pcg.o
    $(CC) $(CFLAGS) $^ -o $@

judge.o: judge.c judge.h
    $(CC) $(CFLAGS) -c judge.c -o judge.o

main.o: main.c judge.h
    $(CC) $(CFLAGS) -c main.c -o main.o

pcg.o: pcg.c judge.h
    $(CC) $(CFLAGS) -c pcg.c -o pcg.o

clean:
    rm -f judge.o main.o pcg.o pcg
  • 运行参数 job.sh
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#!/bin/bash
#SBATCH -o out.txt
#SBATCH --nodes=2
#SBATCH --ntasks-per-node=24 //申请了再说
#SBATCH --cpus-per-task=1
module load openmpi/4.1.5

ulimit -s unlimited
ulimit -l unlimited

make clean
make

mpirun -np 16 -npernode 8 --bind-to core ./pcg ./input_1.bin

  • 尝试绑核

    job.sh 里的 --bind-to core 可以将进程与核心进行一个绑定，绑核对于 OpenMP 程序的性能有很大的影响，在绑核前直接使用 OpenMP 进行循环展开的话会严重降低 OpenMPI 程序的效率（不知为何对 IntelMPI 程序影响比较小🥶），在绑核后进行 reduction 操作就不会严重降低性能了（但还是会降低。因为绑核的失败，所以最后没有采用 OpenMP。

  • 加速效果

    经检测 input_2.bin 和 input_3.bin 的数据也能通过检测。\(6001 \times 6001\) 约 3 分钟， \(8001 \times 8001\) 约 10 分钟。